Eric Colin de Verdière, École normale supérieure, Paris
Autour des décompositions topologiques des surfaces
Comment découper une surface « topologiquement compliquée » (homéomorphe à une sphère à laquelle on recolle des poignées) pour simplifier sa topologie ? Peut-on garantir que la découpe de cette surface ne soit pas trop longue ? Ces questions sont pertinentes pour les problèmes de paramétrage de surfaces (en infographie notamment), comme préliminaire pour résoudre d'autres problèmes topologiques sur les surfaces, et pour l'algorithmique des graphes plongés sur les surfaces.
Je présenterai différents types de décompositions de surfaces : les courbes non contractiles, les graphes de découpe et les décompositions en pantalons. Dans un premier temps, je décrirai des algorithmes efficaces permettant de calculer de telles décompositions aussi courtes que possible, ou au moins avec des garanties sur la longueur. Dans un second temps, je donnerai des bornes inférieures et supérieures sur la longueur de ces décompositions pour des surfaces triangulées, obtenues en utilisant des résultats de géométrie riemannienne et des triangulations aléatoires de surfaces.
Cet exposé survolera plusieurs résultats dûs à Jeff Erickson, Larry Guth, Sariel Har-Peled, Alfredo Hubard, Arnaud de Mesmay, Hugo Parlier, Kim Whittlesey, Robert Young, et l'orateur.
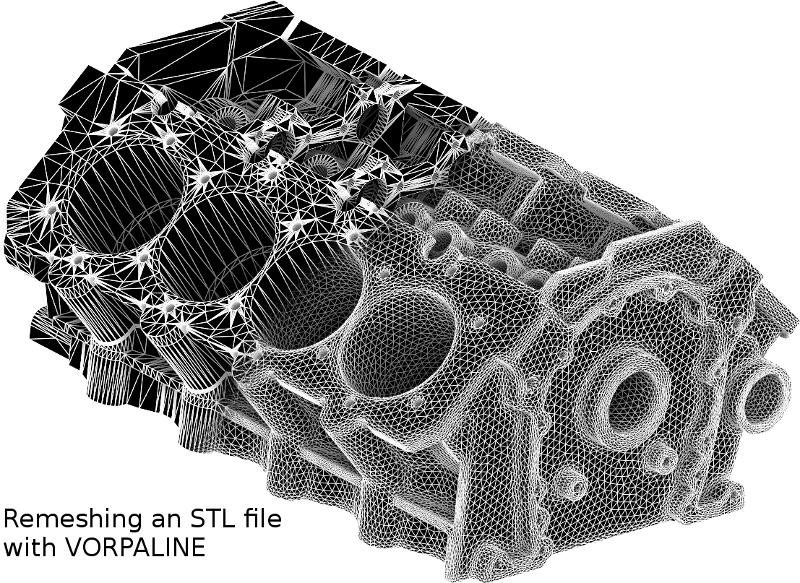
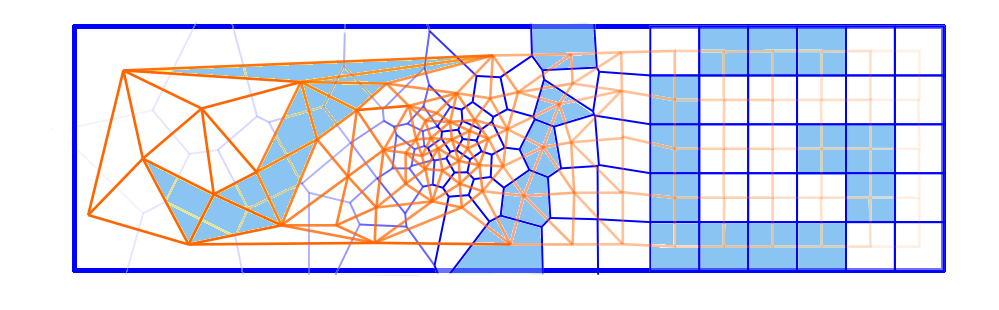
Adrien Loseille, GAMMA3 Project, INRIA Paris-Rocquencourt
Sur un unique opérateur de modification de maillages pour l'adaptation de maillages.
Dans cet exposé, on s'intéresse à l'ensemble des problématiques liés aux maillages qui interviennent dans la simulation numérique: comme le remaillage de surface discrètes ou la génération de maillages anisotropes en 3D, ... Dans ce contexte, on montre qu'on peut définir un modèle de maillage continu hérité des espaces métriques Riemanniens. On décrit ensuite quelques algorithmes pour générer des maillages à partir de leur représentation continue. Ils sont tous basées sur un unique opérateur de cavité. Plusieurs exemples, issus de la mécanique des fluides, montreront des exemples concret d'adaptation.
Victor Ostromoukhov, Université de Lyon 1, CNRS-LIRIS
Méthodes basées sur les pavages pour informatique graphique.
La théorie de pavages intéresse les mathématiciens depuis l’antiquité. Récemment, des applications qui emploient les pavages sophistiqués ont été proposées dans le domaine de synthèse d’image. Dans cette exposé, on fera d’abord l’inventaire des différents types de pavages connus : réguliers, semi- réguliers, non-périodiques, apériodiques. On verra quelles propriétés utiles de ces pavages peuvent être exploitées dans les applications de type échantillonnage de Quasi-Monte-Carlo, en traitement de géométrie etc.
